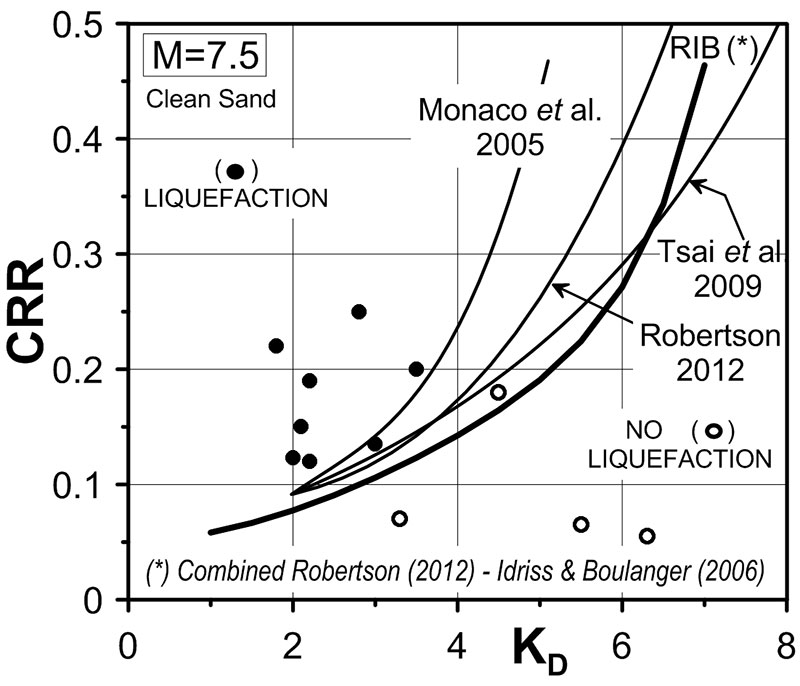
The first studies on a CRR- KD relationship go back to nearly 3 decades ago (Marchetti 1982, Robertson & Campanella 1986). Subsequently, many additional correlations were proposed by various researchers (e.g. Reyna & Chameau 1991, Tsai et al. 2009). A description of the evolution of the correlation can be found in Monaco et al. 2005, who also presented a new correlation.
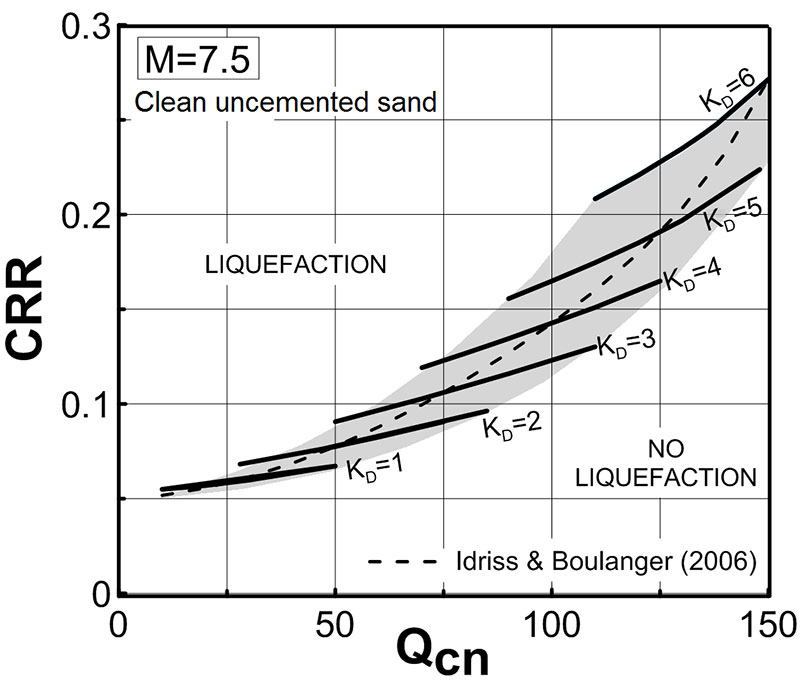
The latest KD -CRR correlations were developed as follows. The starting point was the CPT correlation Qcn -CRR. Then, using the average intercorrelation Qcn – KD, the Qcn parameter in the Qcn -CRR correlation was replaced by KD, thereby obtaining a correlation KD-CRR.
Note that the CPT correlation selected to obtain RIB (i.e. Eqns (1a) & 1(b) combined) has been Eq. (1a). The curve RIB (Fig. 1) is more conservative than Monaco’s.curve (Monaco has sometimes been indicated as a little unconservative).
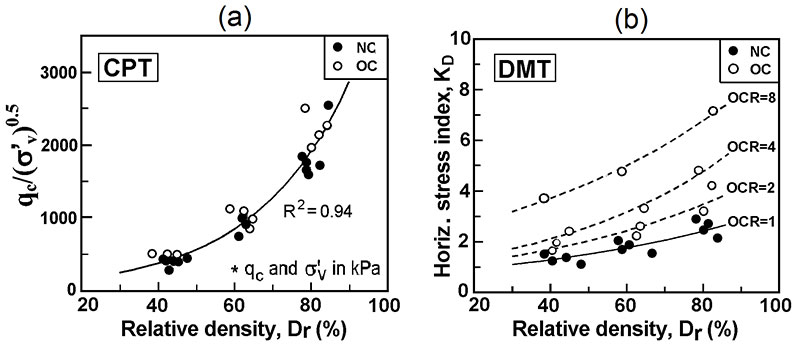
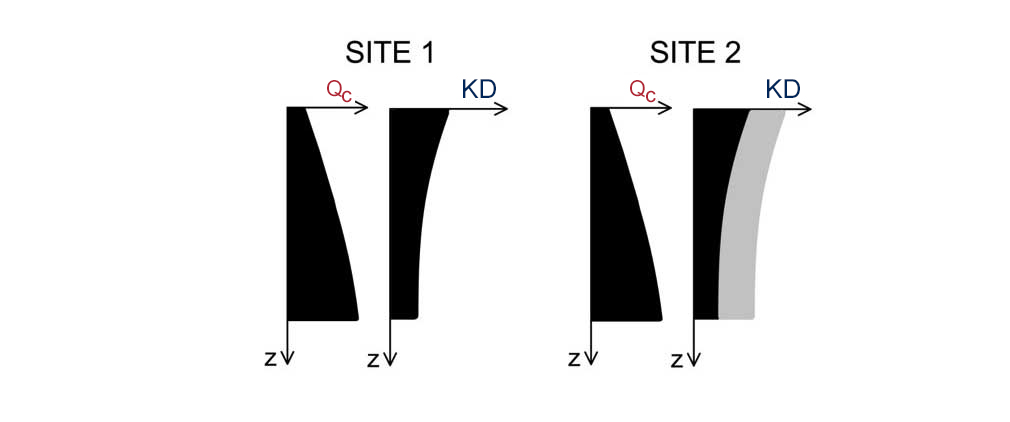
One of the main reasons supporting the use of DMT to assess liquefiability is the significant sensitivity of the DMT’s parameter KD to Stress History – including aging, structure etc. (e.g. Monaco & Schmertmann 2007, Marchetti 2010, Marchetti 2015).Stress history is scarcely felt by qc and, in general, by cylindrical-conical probes (e.g. Huang & Ma 1994). On the other hand Stress History increases significantly CRR. If Stress History is not felt, and therefore ignored, Stress History benefits are wasted, leading to an uneconomical design.
Already in 1985 Jamiolkowski et al. (1985) had warned that “reliable predictions of liquefaction resistance of sands require the development of some new in situ device (other than CPT or SPT), more sensitive to the effects of past stress-strain histories”.
Fig. 3 above provides CRR estimates for clean uncemented sand, but no information in case of appreciable fines or cementation. A possibility to be explored could be the following. Convert Fig. 3 above into a diagram providing the % increase – based on Kd – to be applied to “the best CRR estimate by CPT” (a % diagram, rather than Fig. 3 providing a direct CRR estimate according to current correlations, that in future may be improved). Then apply this % correction factor to “the best CRR estimate by CPT”. The best CRR estimate by CPT is object of continuous improvement by researchers, including the fines correction. As CPT researchers improve “the best CRR estimate by CPT”, the CRR prediction would be automatically updated by applying the % factor to “the best CRR estimate by CPT” inclusive of the fines correction.