Modulus M
It is well known that oedometer moduli M are not constant, but vary with the applied vertical load. In particular the oedometer modulus increases up to the maximum past pressure pc. At pc , break point in the e-log p curve, the modulus decreases, to increase again at higher loads. Therefore the average modulus to be used for predicting settlement should in principle be chosen as the average modulus in the interval between the initial and the final vertical load. This can be done if the e-log p curve from the oedometer is available, but cannot be done if only the constrained modulus at geostatic stress is available. Since the target of DMT is specifically the 1-D modulus at vertical geostatic stress, and since DMT does not provide information on modulus at stresses higher than geostatic, predicting settlements using MDMT involves approximation. Fig. 4 shows schematically two typical e-log p oedometer curves, and the values of the moduli M at various applied vertical load p. In many natural soils, with the exception of highly structured clays, where the break is sharp, the variation of the modulus across pc is moderate. Hence the error in assuming M≈constant is often relatively acceptable for practical purposes. This assertion is supported by the large number of case histories in the recent decades indicating good agreement between observed and DMT-predicted settlements. On the other hand moduli estimated by alternative methods are not rarely affected by errors (e.g. disturbed samples) much larger than the mentioned approximation.
It is reminded that MDMT provides an estimate of the operative modulus during the consolidation. Hence the predicted settlement is the primary settlement, and does not include the secondary settlement.
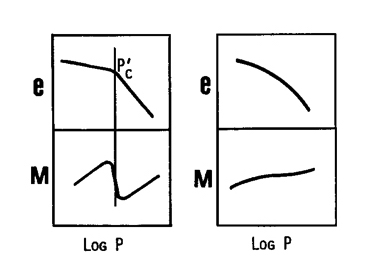
Schematic variation of the oedometer moduli with applied load.
In clay, the expansion of the membrane occurs in undrained conditions. Therefore the dilatometer modulus ED is an undrained modulus. Thus, according to logic, the correlation to be investigated should be between ED and the undrained modulus Eu. Attempts of this kind were carried out in the early days of the DMT development. However a big obstacle, precluding such possibility, was the high variability of the undrained moduli provided by different laboratories, at least in part due to the high sensitivity of Eu to the disturbance. Hence, as a second attempt, the correlation ED – M was investigated. This correlation involves many soil properties, including material type, anisotropy, pore pressure parameters etc. Hence no unique ED – M correlation can be expected. On the other hand the DMT provides, in addition to ED, also the parameters ID and KD , containing at least some information on material type and stress history. This availability provides some basis to expect at least some degree of correlation ED – M , using ID and KD as parameters. Moreover, while the correlation ED – M is, at least in principle, weaker than ED – Eu , at least ED – M can be tested, because M by different laboratory have much less variability than Eu.
Obviously the final word goes to real world observations. Large number of case histories have generally proved the favorable comparisons between observed and DMT-predicted primary settlements, thereby supporting the use of MDMT as operative constrained modulus.
Note also Lambe et al. (1977 Jnl Asce GE, 106, GT3): “Drained moduli of saturated clays are typically about one-third to one-fourth the undrained values”. Hence a broad connection drained-undrained stiffness has already been invoked in the past.
Settlements calculations are generally carried out using the 1-D elasticity formula in 1-D problems, say large rafts, or the 3-D elasticity formula in 3-D problems, say small isolated footings. The well known formulae are respectively:
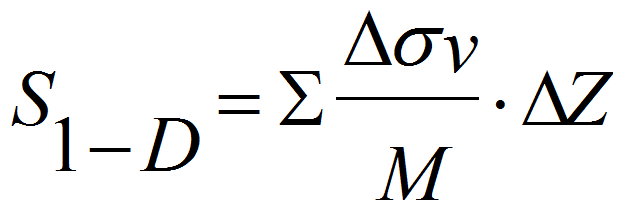
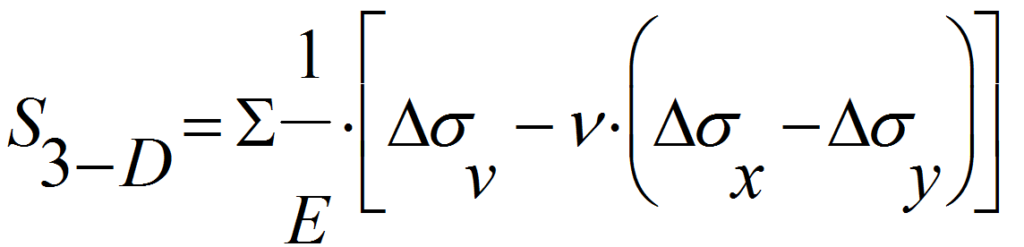
However the general recommendation is to use in all cases the 1-D formula, for the following reasons (Marchetti, 1991):
- The 3-D formula (unlike the 1-D) involves Poisson’s ratio n (unknown) and makes use of the horizontal stresses sh that “may be grossly over-/underestimated by theory of elasticity”, while the vertical stresses “are surprisingly well predicted by simple elastic theory”
- In most cases the 1-D formula gives settlements that are within 10% of the 3-D calculated settlements, because of the following compensation: M in Eq. 10 is higher than E in Eq. 11, but Eq. 11 contains a negative term
- Errors due to the formulae are small compared with errors in deformation parameters. As noted by Poulos: What is important is the modulus, not the formula.
Since the above two formulae give similar answers, it appears preferable to use the 1-D formula, simpler and avoiding elusive n or σh.