Predicting settlements of shallow foundations
Table of Contents
Add a header to begin generating the table of contents
Predicting settlements of shallow foundations is the No. 1 application of the DMT, especially in sands, where undisturbed samples cannot be retrieved. Many world experts consider DMT one of the best presently available tool for predicting settlements, notoriously not well predicted by conical probes.
Settlements are generally calculated, both in sands and in clays, by means of the one-dimensional formula.
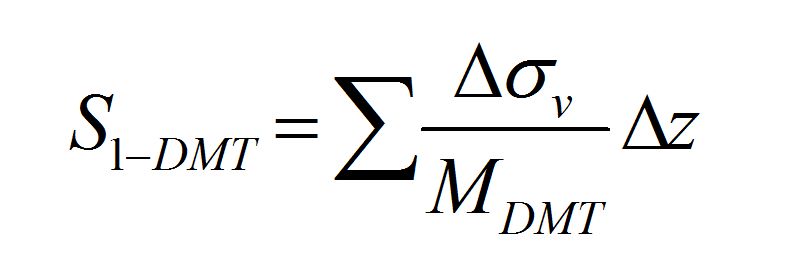
Where Dsv is calculated according to Boussinesq and MDMT is the constrained modulus by DMT. In clays the predicted settlement is the primary settlement (net of immediate and secondary).
The validity of the method has been confirmed by a large number of observed agreement between measured and DMT-predicted settlements. (see e.g. summaries of comparisons by Schmertmann 1986, Monaco et al. 2006, Failmezger 2015).
Settlements estimates are useful, for instance, when the designer has to choose between a shallow foundation and a piled foundation.
A computer program for calculating settlements according to Eq. 1 is freely available. The DMT Settlements Software is freely downloadable in the section SOFTWARE.
The validity of the method has been confirmed by a large number of observed agreement between measured and DMT-predicted settlements. (see e.g. summaries of comparisons by).
Settlements estimates are useful, for instance, when the designer has to choose between a shallow foundation and a piled foundation.
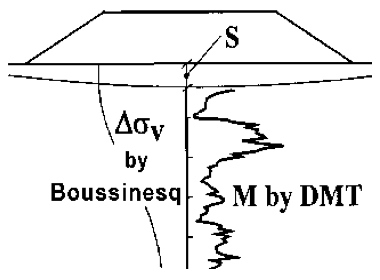
The dilatometer modulus ED should not to be used, as such, for predicting settlements, because ED is only slightly sensitive to Stress History, while the operative modulus increases considerably with Stress History. ED must first be corrected for Stress History:
where ED is the dilatometer modulus and RM is a correction factor applied to ED depending primarily on the stress history index KD (Marchetti 1980). As to the operative Young’s modulus E, if required, it can be estimated from Mdmt using the theory of elasticity (E ≈ 0.8-0.9 MDMT).
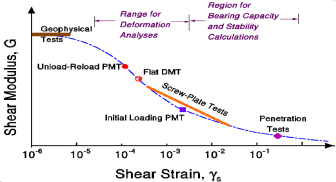
Incorporating stress history information in the settlement calculation, using KD, is not a refinement, but a necessity. The availability of the parameter KD is important. There are not many alternatives to KD for obtaining in situ information on stress history. On the other hand if the investigation is carried out with probes of modest sensitivity to stress history, the benefits of stress history are ignored, leading to a settlement overprediction and a more expensive design.
If purpose is parameters, CPT cannot be used in isolation – must be supplemented by laboratory or other methods. CPT can easily mislead in terms of soil type, strength and particularly modulus.
Roger A. Failmezger, P.E., F. ASCE, D GE – In-Situ Soil Testing, L.C., Lancaster, Virginia, U.S.A.
| Project Name | Cost Savings with DMT Redesign of Foundation System |
|---|---|
| Westminister Village | $100,000 |
| Ocean Landing Shopping Center | $750,000 |
| Old Town Crescent | $150,000 |
| Fox Run Village | $100,000 |
| Monarch Landing | $150,000 |
| MD Live! | $2,000,000 |
| Towson Circle | $200,000 |
| Retirement Community, Glen Mills, PA | $150,000 |
| Xfinity Live! | $500,000 |
| Obery Court | $200,000 |
| Residences at Rivermarsh | $100,000 |
| Residences at River Place | $80,000 |
| Ocean Pines | $200,000 |
| Four Seasons | $100,000 |
| 912 King Street-116 S Henry Street Mixed Use | $500,000 |
| Dumfries Town Square | $200,000 |
| Seacobeck Hall—Mary Wash- ington University | $500,000 |
| Motown | $150,000 |
| Richmond Area Collegiate Sci- ence Building | $85,000 |
| Richmond Area Collegiate Re- search Building | $150,000 |
| Food Processing Addition and Tank Farm | $100,000 |
| 13th and U Street | $100,000 |
| 55 M Street | $150,000 |
| Alexan Dunn Loring Develop- ment | $250,000 |
| Association of Manufacturing Technology Building | $150,000 |
| Excelsior Parc Development | $100,000 |
| Glenmont WMATA | $150,000 |
| Halley Rise | $150,000 |
| Howard Hughes HHMI Expan- sion | $100,000 |
| I-64 Widening | $500,000 |
| JHU-NIH-NCI | $150,000 |
| Mark Center Plaza Building 5 | $150,000 |
| Mosaic Parcel CE | $100,000 |
| National Gateway Land Bay “E” West | $250,000 |
| Potomac Yard Bay D | $150,000 |
| Ripley Street Development | $100,000 |
| Rock Spring Centre | $250,000 |
| Route 7 over Dulles Toll Road | $150,000 |
| Route 7 Widening | $350,000 |
| Tysons Archstone | $150,000 |
| Tysons Central | $250,000 |
| Upper Rock Blocks G & H | $100,000 |
| West Falls Church WMATA | $150,000 |
| McWane Hall—Lynchburg Col- lege | $100,000 |
| Brooktrout | $50,000 |
| Mecklenburg Schools | $100,000 |
| Abingdon Elementary School | $225,000 |
| Abingdon Heights | $400,000 |
| Fauquier High School | $250,000 |
| Prince William Commons | $400,000 |
| PWCPS Administration Bldg | $225,000 |
| Warrenton Aquatic & Recrea- tion Facility | $250,000 |
| Washington Center | $350,000 |
| WMATA White Flint Parking Garage | $625,000 |
| 3800 Glenwood | $350,000 |
| Homewood Suites | $150,000 |
| Johnson County WWTP | $1,000,000 |
| 1011 M Street | $200,000 |
| 14th and W Street | $200,000 |
| 1600 7th Street | $50,000 |
| 300 8th Street | $125,000 |
| A-1 Glass | $100,000 |
| B-CC High School | $350,000 |
| Carlisle | $200,000 |
| Fairfax Blvd Center | $100,000 |
| Forest Oak Middle School | $100,000 |
| Grimke | $1500,000 |
| Kilmer Place | $50,000 |
| Liberty Tank | $100,000 |
| Sumner Suites | $125,000 |
| Windsor | $50,000 |
| Wood Middle School | $75,000 |
| Wootton | $75,000 |
| 14th and P Street | $150,000 |
| Culpepper Farmers’ Coop | $50,000 |
| Indian Head Water Tanks | $75,000 |
| Portals Phase 3 | $175,000 |
| Thomas Jefferson Library | $75,000 |
| Avalon Mosaic Parcel H | $800,000 |
| Cabin John Middle School | $200,000 |
| Navy Federal Credit Union | $100,000 |
| Cambridge Village | $150,000 |
| Ben Oaks Water Tower | $75,000 |
| Apple Greene Water Tower | $50,000 |
| Oyster Bay Condos | $100,000 |
| North Beach Various Parcels | $50,000 |
| Fort Meade-DINFOS | $200,000 |
| Fort Meade-Building #8605 | $50,000 |
| Fort McNair-Building #48 | $250,000 |
| 535 Broadwater Road | $50,000 |
| 15 Judith Sound Circle | $8,000 |
| 318 Ironside Circle | $50,000 |
| Courthouse Professional Build- ing | $60,000 |
| Dahlgren Hotel | $75,000 |
| Doc Stone MOB | $40,000 |
| Hamptons at Hunton Park | $60,000 |
| Kaeser Compressors Warehouse Expansion | $80,000 |
| New Post Site | $50,000 |
| Oakwood Estates | $85,000 |
| Sophia and Hanover Streets | $40,000 |
| 1112 First Street Hotel | $250,000 |
| Courthouse Village Bridge | $250,000 |
| Arbor House | $100,000 |
| William Square Hotel | $250,000 |
| James Madison University— Phillips Hall | $150,000 |
| 1336 H Street | $80,000 |
| Reston Crescent | $90,000 |
| Total Cost Savings | $21,258,000 | ||